Discrete How to Know Which Proof to Use

Thus the sum a b may be re-written as. Suppose a and b are odd.

Intro To Proofs Discrete Math Structures 3 Youtube

A if and only if B means that you must prove that A and B are logically equivalent.

. If A then B statements mean that you must prove whenever A is true B must also be true. Ii On the next line write the word proof - it is from this point onward you shall start to write your proof. These are phrases that you need to be familiar with and know how to use properly when writing your own proof.

To be a discrete random variable you should be able to select two potential outcomes and know there are no outcomes between those two. Prove P implies Q and not P implies not Q. We learn how to do formal proofs in set theory using intersections unions complements and differences000 - Intro049 - Language of Set Theory331 -.

However in proof by contrapositive you end at the negated hypothesis whereas proof by contradiction ends at some contradiction that may not be closely related to the statement of the original claim. A B C D. Now n 2 4 k 2 2 2 k 2 these algebraic manipulations are examples of modus ponens.

Truth and falsity are mutually exclusive so that. Proof by contrapositive and proof by contradiction. I This implies that the original implication is a tautology.

I To summarize to prove the implication A B by contradiction we assume the hypothesis A and the negation. Disproving false propositions having conclusions of the form xPx Qx 114. Then Q is a syththony.

I am sure everyone knows this fact but only few actually know the proof. Consider the Pythagoras theorem most famously know as c2 a2 b2. Steps to a direct proof the second step is of course the tricky part.

If Atext Btext and C are sets then Acap B cup C Acap B cup A cap Ctext Proof. P q where p is a contradiction. In fact there are many proofs for the Pythagoras theorem and you are encourage to find one either on your own or by doing some little research.

In order to prove this two steps are needed Prove existence and Prove Uniqueness. Assume for the sake of contradiction that there are integers x and y such that x is a prime greater than 5 and x 6y 3text End of proof. Thus if n is odd n2is also odd.

This is a basic rule of logic and proof by contradiction depends upon it. With a number of different types of proofs available it can be difficult in choosing the best type of proof to use. Deducing conclusions having the form For everyxifPx thenQx 11.

Let n be an integer. Because n is even n 2 k for some k k is existentially quantified defined in terms of n which appears previously. In this Guide will help you understand better the proofs you read.

Direct Vs Indirect Proof. Iii Clearly mark the end of your proof with QED or some other such symbol this is especially important if you are proving. Consider an arbitrary ichenochen J.

Indirect proof includes two proof methods. The Distributive Law of Intersection over Union. The example given is Show that if a and b are real numbers and a 0 then there is a unique real number r such that a r b 0.

Prove both if A then B and if B then A. I could do the existence portion. Let Q be an oaaa.

Try to proveQx where Qx Px but the has been moved to the right by DeMorgan. Assume n is an even number n is a universally quantified variable which appears in the statement we are trying to prove. Ab 2k 12m 1 4km 2k 2m.

In general wherever possible in a proof try to replace predicates by their definitions. If ab is an even number then a or b is even. Note that this sep-arates the statement of the theorem from the proof so should help avoid any confusion.

R b a I would like some clarification on proving the uniqueness part. Propositions having one or more hypotheses 113. That is a 2k 1 and b 2m 1 for some integers k and m.

Is l Dillig CS311H. Some kind of proof goes here. Px where Px is a compound proposition.

To perform a direct proof we use the following steps. Discrete Mathematics Mathematical Proof Techniques 731. Prove P implies Q and Q implies P.

Because a and b are consecutive we know that b a 1. Some kind of proof goes here. Assume that a and b are consecutive integers.

Direct proofs always assume a hypothesis is true and then logically deduces a conclusion. State or restate the theorem so you understand what is given the hypothesis and what you are trying to prove the conclusion. P q must be true.

Consider the result of a fair six-sided die roll The. In contrast an indirect proof has two forms. Use P to show that Q must be true.

In both you start from the negated conclusion of the original claim. Assume n is a multiple of 3. Assume that P is true.

Then n2 4 k 4 k 1 22 k22 k1 which is odd. Construct a chain of if and only if statement. This is a simple guide that can help decide which type of proof might be best to prove your statementGuide to Selecting a Proof Method.

Identify the hypothesis and conclusion of the conjecture youre trying to prove Assume the hypothesis to be true Use definitions properties. Decide which of the following are valid proofs of the following statement. If a and b are consecutive integers then the sum a b is odd.

We can use several methods or techniques in building a proof but there are two major groups. Propositions having no hypothesis 112. More Direct Proof Examples.

But heres a false proof. By de nition of oddness there must exist some integer k such that n 2 k 1. For an integer n n is even if and only if n2 is even.

We learn how to do formal proofs in set theory using intersections unions complements differences and cartesian products or cross products000 - Intr. Every ichenochen is a zichenzochen. A mathematical proof is a deductive argument for a proposed statement.

Indirect Proof Proof by Contradiction I Recall that A B A_B I The negation of this disjunction is AB I To prove the original implication we show that its negation is a contradiction. This is a contradiction so there are no such integers. IProofAssume n is odd.

A statement cannot be true and false at the same time If the statement can be proven true then it cannot be false If the statement can be proven false then it.

Discrete Math Induction Proof For Summation Mathematics Stack Exchange

Discrete Math Logic When Is A Proof Finished Stack Overflow

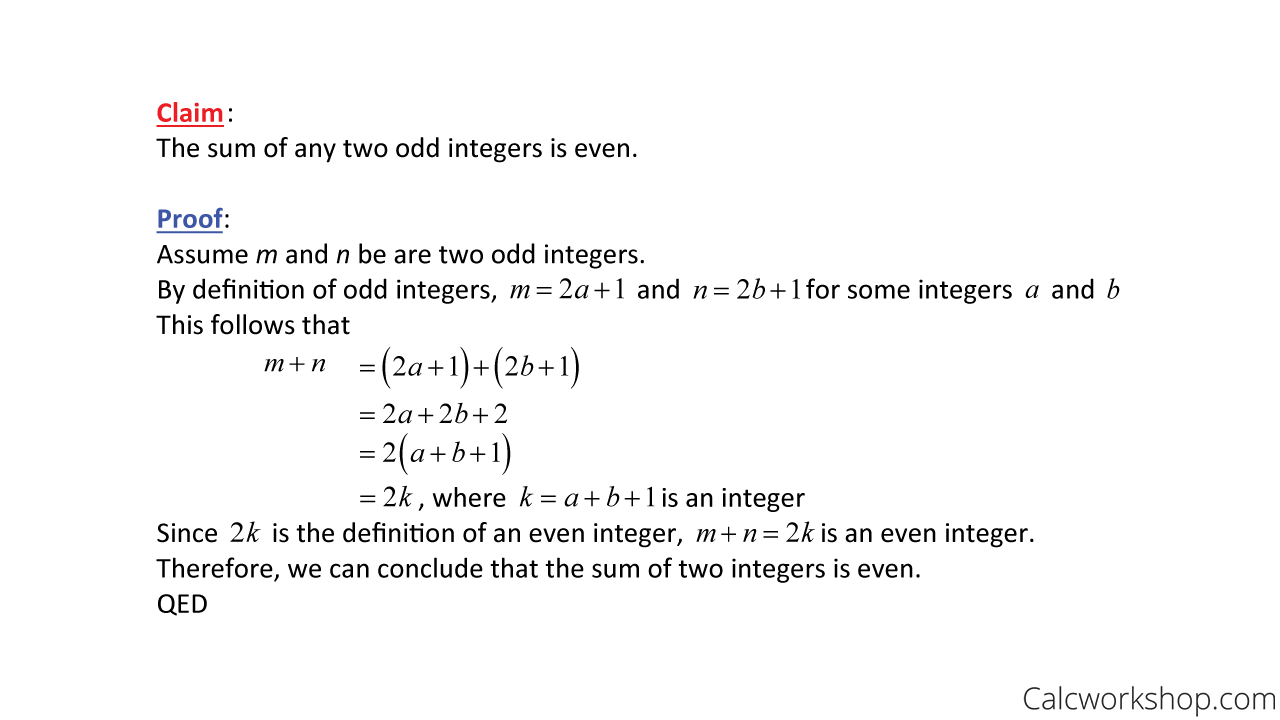
Direct Proof Explained W 11 Step By Step Examples

Inequality Discrete Math Proof Of Inequalities Mathematics Stack Exchange